Vesihöyrypitoisuus#
Julkaistu alunperin 2020-08-09
Edellisessä kirjoituksessa käsittelimme suhteellisen kosteuden määritelmää. Siinä esiintyi yhtenä terminä vallitseva vesihöyrypitoisuus, joka on tämän kirjoituksen pääaihe.
Määritelmä#
Vesihöyrypitoisuus kuvaa ilmassa kunakin ajanhetkenä olevan vesihöyryn määrän. Rakennusfysiikassa vesihöyrypitoisuus ilmaistaan yleensä ilmatilavuutta kohti, jolloin merkintänä on \(\nu\) ja yksikkö on joko kg/m\(^3\) tai g/m\(^3\). Talotekniikan puolella vesihöyrypitoisuus ilmaistaan usein massaosuutena kuivaa ilmaa kohti, jolloin merkintänä on \(\varepsilon\) ja yksikkönä kg/kg tai g/kg. Muunnoskaava näiden kahden välille voidaan kirjoittaa asettamalla ehto, että ilmatilavuudessa \(V\) vesihöyryn massa \(m_{\nu}\) on sama kummallakin tavalla ilmaistuna. Tällöin saadaan:
…ja josta edelleen:
Suure \(m_{ki}\), kg on tilavuuden \(V\), m\(^3\) sisään jäävän kuivan ilman massa, joka taas voidaan kirjoittaa kuivan ilman tiheyden \(\rho_{ki}\), kg/m\(^3\) ja tarkasteltavan tilavuuden \(V\) tulona. Kuivan ilman tiheys on noin 1,2 kg/m\(^3\) lämpötilassa 20 \(^\circ\)C ja 1,4 kg/m\(^3\) lämpötilassa -30 \(^\circ\)C.
Keski-Euroopassa vesihöyryn määrä ilmassa ilmaistaan usein vesihöyryn osapaineena \(p_{\nu}\), Pa. Muunnos vesihöyryn osapaineen ja vesihöyrypitoisuuden välillä voidaan tehdä ideaalikaasun tilanyhtälön avulla seuraavasti:
Tällöin \(R_w\) on veden ominaiskaasuvakio 461,5 J/(kg, K) ja \(T\) on vesihöyryn lämpötila, K. Ideaalikaasun kokonaispaine on osapaineiden summa, mutta kaasun lämpötila on sama kaikille osakaasuille.
Esimerkki: Vesihöyryn osapaine on 1000 Pa. Kun kaasun lämpötila samaan aikaan on 20 \(^\circ\)C, niin vesihöyrypitoisuus on tällöin \(\nu\) = 1000 Pa / (461,5 J/(kgK) \(\cdot\) (273,15 + 20) K) = 0,0074 kg/m\(^3\) = 7,4 g/m\(^3\). Jos kuivan ilman tiheys on 1,2 kg/m\(^3\), niin kosteuspitoisuus massaosuutena on \(\varepsilon\) = 0,0074 kg/m\(^3\) / 1,2 kg/m\(^3\) = 0,0062 kg/kg = 6,2 g/kg.
Esimerkki vesihöyryn määrästä huoneilmassa#
Tarkastellaan esimerkkinä asuinhuonetta (\(V\) = 50 m\(^3\)), jossa pyykin kuivaamisen seurauksena huoneilman keskimääräinen vesihöyrypitoisuus nousee arvosta \(\nu\) = 6 g/m\(^3\), arvoon \(\nu\) = 8 g/m\(^3\). Tällöin ennen pyykin kuivausta huoneilmassa oli vesihöyryä \(m\) = 50 m\(^3\) \(\cdot\) 6 g/m\(^3\) = 300 g ja pyykinkuivauksen aikaan \(m\) = 50 m\(^3\) \(\cdot\) 8 g/m\(^3\) = 400 g. Huoneilmassa olevan vesihöyryn määrä kasvoi siis 100 g.
Jos huoneilman lämpötila on vaikkapa 22 \(^\circ\)C, niin tällöin aikaisemman kirjoituksen mukaisesti kyllästysvesihöyrypitoisuus on tällöin 19,4 g/m\(^3\). Jos huoneen lämpötila pysyy pyykin kuivauksen ajan vakiona, niin tällöin suhteellinen kosteus ennen kuivausta olisi \(\varphi\) = 6 g/m\(^3\) / 19,4 g/m\(^3\) = 0,31 = 31 %. Pyykin kuivauksen aikaan huoneilman suhteellinen kosteus on \(\varphi\) = 8 g/m\(^3\) / 19,4 g/m\(^3\) = 0,41 = 41 %.
Kosteuden haihduttaminen pyykeistä sitoo lämpöä huoneilmasta, jolloin huoneilman lämpötila laskee hieman (kun huonetermostaatit eivät ole vielä ehtineet mukaan). Jos huoneilman lämpötila laskee vaikkapa arvoon 21 \(^\circ\)C, niin tällöin vesihöyryn kyllästysosapaine olisi 2481 Pa, eli 18,3 g/m\(^3\). Tällöin pyykkiä kuivattaessa huoneilman suhteellinen kosteus olisi \(\varphi\) = 8 g/m\(^3\) / 18,3 g/m\(^3\) = 44 %.
Edellä oleva laskelma ei ota huomioon sitä, että huonetiloissa on käytännössä aina vähintään pieni ilmanvaihto, eli että huoneeseen tulee ilmaa ulkoa ja/tai viereisistä huoneista, ja että ilmaa lähtee huoneesta pois ulos ja/tai viereisiin huoneisiin. Käsitellään tämä tilanne seuraavassa taseyhtälön avulla.
Vesihöyryn taseyhtälö#
Tässä yhteydessä taseyhtälöllä tarkoitetaan massan säilymislakia kirjoitettuna seuraavaan muotoon:
”varaston muutosnopeus” = ”tulevat kosteusvirrat” – ”lähtevät kosteusvirrat”
Jatketaan edellä olleen huoneen tarkastelua hieman eri näkökulmasta ja sanotaan, että huoneeseen tulee ikkunaventtiilien läpi ulkoilmaa 5 L/s (litraa sekunnissa) ja huoneiston välioven kynnyksen alta siirtoilmaa 3 L/s. Huoneesta on koneellinen poisto, joka vie siis tällöin 8 L/s ilmaa mukanaan. Ulkoilman vesihöyrypitoisuus olkoon 4 g/m\(^3\). Viereisen huoneen vesihöyrypitoisuus on sama kuin tarkasteltavassa huoneessa ennen pyykinkuivauksen aloittamista, eli 6 g/m\(^3\). Pyykistä kuivuu 5 kg vettä 24 h aikana. Pyykin kosteustuotto huonetilaan olkoon tätä esimerkkiä varten vakiosuuruinen 5 kg/24 h = 0,058 g/s.
Ilmavirran mukanaan kuljettama kosteusvirta \(G\), kg/s lasketaan seuraavasti:
Jos ilmavirtaus kulkee lähtöpisteestä 1, maalipisteeseen 2, niin kaavassa käytetään vesihöyrypitoisuutena lähtöpisteen 1 vesihöyrypitoisuutta \(\nu_1\). Suure \(q_v\), m\(^3\)/s on tilavuusilmavirtaus. Piirretään seuraavaksi tarkasteltavasta tilanteesta kuva (piirrä kuva!).
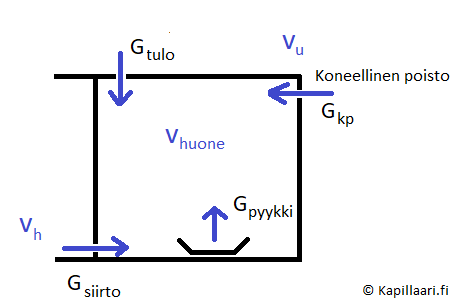
Fig. 6 Kosteusvirrat G ja vesihöyrypitoisuudet \(\nu\). Kaikki kosteusvirrat on laitettu kuvaan positiivisiksi huonetta kohti.#
Kuvaan on laitettu harjoituksen vuoksi myös koneellinen poisto huonetta kohti, vaikka sen tiedetään kohdistuvan huoneesta pois. Tämä on tehty sitä varten, että nyt kosteusvirtojen suuntia ei tarvitse arvailla etukäteen (ellei halua) ja niiden suunnat tulevat suoraan kaavoista.
Joka tapauksessa nyt voidaan kirjoittaa taseyhtälö auki huoneessa olevan vesihöyryn määrän muutosnopeudelle:
varaston muutosnopeus = \( G_{siirto} + G_{tulo} + G_{pyykki} + G_{kp} \)
Sijoittamalla kosteusvirran lausekkeet saadaan:
varaston muutosnopeus = \( \nu_h q_{v,h} + \nu_u q_{v,u} + G_{pyykki} + \nu_{huone} q_{v,kp} \)
Sijoittamalla lukuarvot kuivumisen alkuhetkellä saadaan:
varaston muutosnopeus
= 6 g/m\(^3\) \(\cdot\) 0,003 m\(^3\)/s + 4 g/m\(^3\) \(\cdot\) 0,005 m\(^3\)/s + 0,058 g/s + 6 g/m\(^3\) \(\cdot\) (-0,008 m\(^3\)/s)
= 0,018 g/s + 0,020 g/s + 0,058 g/s – 0,048 g/s
= 0,048 g/s.
Huoneilman sisältämän vesihöyryn määrä kasvaa siis pyykinkuivauksen alussa vauhdilla 0,048 g/s. Lukuarvo oli sama, kuin koneellisen poiston mukanaan viemä kosteusvirta, mikä oli hauska sattuma!
Oletetaan tilanteen jatkuvan vaikkapa 15 minuuttia, jona aikana huoneilmassa olevan kosteuden määrä on kasvanut: 15 min \(\cdot\) 0,048 g/s = 15 \(\cdot\) 60 s \(\cdot\) 0,048 g/s = 43,2 g.
Huoneen ilmatilavuus oli 50 m\(^3\), joten huoneilman keskimääräinen vesihöyrypitoisuus on kasvanut 43,2 g / 50 m\(^3\) = 0,86 g/m\(^3\). Koska alkutilanteen vesihöyrypitoisuus oli 6 g/m\(^3\), niin uusi vesihöyrypitoisuus on (6 + 0,86) g/m\(^3\) = 6,86 g/m\(^3\).
Tämä tieto voidaan nyt päivittää aikaisempaan laskelmaan ja laskea uusi muutosnopeus huoneilmassa olevan vesihöyryn määrälle:
varaston muutosnopeus
= 6 g/m\(^3\) \(\cdot\) 0,003 m\(^3\)/s + 4 g/m\(^3\) \(\cdot\) 0,005 m\(^3\)/s + 0,058 g/s + 6,86 g/m\(^3\) \(\cdot\) (-0,008 m\(^3\)/s)
= 0,018 g/s + 0,020 g/s + 0,058 g/s – 0,055 g/s
= 0,041 g/s.
Huoneilmassa olevan vesihöyryn määrä kasvaa nyt (t = 15 min) siis hieman hitaammin, kuin kuivumisen alussa (t = 0 min), eli 0,041 g/s \(\lt\) 0,048 g/s. Uudella muutosnopeudella vesihöyryn määrä huoneilmassa kasvaa seuraavan 15 min aikana: 15 \(\cdot\) 60 s \(\cdot\) 0,041 g/s = 36,9 g.
Puoli tuntia kuivumisen alusta huoneilman vesihöyrypitoisuus on siis: 6,86 g/m\(^3\) + 36,9 g / 50 m\(^3\) = 6,86 g/m\(^3\) + 0,74 g/m\(^3\) = 7,6 g/m\(^3\).
Vesihöyrypitoisuus vaikuttaa nousevan laskuesimerkissä aika voimakkaasti. Jätetään laskentaan liittyvien virhelähteiden arviointi ja tulosten luotettavuuden arviointi kuitenkin toiseen blogikirjoitukseen.
Yhteenveto#
Tässä kirjoituksessa käytiin läpi eri merkintätapoja ilman vesihöyrypitoisuudelle ja esimerkkilaskelma pyykinkuivauksen vaikutuksesta huoneilman vesihöyrypitoisuuteen. Massan säilymislakia soveltamalla on mahdollista kirjoittaa lausekkeet monenlaisten tehtävien ratkaisemiseksi. Lisäksi perusperiaatteiden tiedostaminen auttaa hahmottamaan eri ilmiöiden käyttäytymistä, vaikka tarkkoja vastauksia ei aina pystyisikään antamaan.
