Mittausepävarmuuden laskeminen ja ilmoittaminen

Julkaistu alunperin 2020-11-01.

Takaisin etusivulle

Mikään mittaustulos ei ole täydellisen tarkka, vaan saatu tulos sisältää aina erilaisia mittausepävarmuuksia. Nämä mitattujen arvojen epävarmuudet ovat läsnä myös niiden perusteella tehtyjen laskelmien tuloksiin. Tämän kirjoituksen tarkoituksena on käydä ensin läpi muutamia tilastomatematiikan peruskäsitteitä, joita tarvitaan mittausepävarmuuksien käsittelyyn. Tämän jälkeen käydään läpi GUM-oppaassa esitetty tapa mittausepävarmuuksien laskemiseen ja esittämiseen. Lopuksi käydään läpi lyhyt esimerkki U-arvolaskennan tulokseen liittyvän standardiepävarmuuden laskennasta.

Satunnaismuuttuja

Satunnaismuuttuja (random variable) on muuttuja, jonka lukuarvo määräytyy satunnaisilmiön perusteella. Kyseessä voi olla diskreetti tai jatkuva muuttuja. Diskreetit muuttujat voivat saada vain tiettyjä kokonaislukutyyppisiä arvoja, kuten kruuna tai klaava kolikonheitossa, nopan silmäluku nopanheitossa, maalien määrä jalkapallopelissä tai ihmisten lukumäärä rakennuksessa. Jatkuvat satunnaismuuttujat voivat saada esiintymisalueeltaan mitä tahansa reaalilukuarvoja ja tällaisia ovat esimerkiksi rakennuksen toteutunut ostoenergiankulutus, lämmöneristeen paksuus vanhassa betonisandwichpaneelissa ja höyrynsulun vesihöyrynvastus.

Monet mittalaitteet antavat mittaustulokset yleensä jollakin äärellisellä resoluutiolla, mutta tässä yhteydessä jatkuvalla satunnaismuuttujalla ei tarkoiteta mittalaitteesta luettua, portaittain vaihtelevaa tulosta, vaan tämän taustalla olevan ilmiön todellista arvoa.

Satunnaismuuttujiin liittyvät merkintätavat vaihtelevat jonkin verran kirjallisuuslähteestä toiseen ja näin tapahtuu myös tämän kirjoituksen sisällä. Pääosin merkintavoissa on käytetty periaatetta, että satunnaismuuttujaa on merkattu isolla kirjaimella (\(X\) tai \(Y\)), kun taas satunnaismuuttujan saamaa arvoa on merkitty vastaavalla pienellä kirjaimella (\(x\) tai \(y\)). Funktiolla \(f\) on tarkoitettu tekstin alkupuolella todennäköisyysjakaumaa, mutta tekstin loppupuolella mitä tahansa tietyn ilmiön määrittävää funktiota. Tarkan merkityksen pitäisi kuitenkin käydä ilmi kontekstista ja tekstiin linkitetyistä lähteistä.

Todennäköisyysjakauma

Yleistä

Satunnaismuuttujan saamien arvojen vaihtelua kuvataan todennäköisyysjakaumalla. Todennäköisyysjakauma kuvaa satunnaismuuttujan eri arvojen yleisyyttä.

Diskreetin satunnaismuuttujan tapauksessa tarvitaan diskreettejä pistetodennäköisyysjakaumia. Nämä on mahdollista määrittää yksinkertaisimmillaan taulukoimalla eri mahdollisuudet ja määrittämällä sen jälkeen kutakin tapausta vastaava esiintymistodennäköisyys.

Jatkuvien satunnaismuuttujien tapauksessa tarvitaan jatkuvia todennäköisyysjakaumia. Näitä on mahdollista approksimoida histogrammi-tyyppisillä taulukoiduilla arvoilla, mutta yleisempi tapa on käyttää analyyttisia tiheysfunktioita. Kaksi tunnetuinta jatkuvaa tiheysfunktiota ovat tasajakauma ja normaalijakauma. Lisäksi joskus voi olla perusteltua käyttää kolmiojakaumaa, minkä lisäksi se toimii hyvänä esimerkkinä siitä, että kirjallisuudesta löytyy paljon erilaisia jakaumia. Siinä missä diskreetit todennäköisyysjakaumat (probability mass function, pmf) antavat suoraan eri arvojen esiintymistodennäköisyyksiä, todennäköisyystiheysfunktioista (probability density function, pdf) todennäköisyyksiä saadaan vasta integroimalla tiheysfunktiota \(x_1\):stä \(x_2\):een.

Todennäköisyysjakaumilla on monia ominaisuuksia, mutta nostetaan tässä esille vain yksi: Sekä diskreetin että jatkuvan todennäköisyysjakauman integraalin tulee olla yksi (1). Diskreetille jakaumalle tämä lasketaan summaamalla yhteen kaikkien jakauman arvojen pistetodennäköisyydet:

\[ \sum_{i=1}^{n} f \left( x_i \right) = 1 \]

jossa muuttuja \(i = 1...n\) käy läpi kaikki mahdolliset esiintyvät tapausvaihtoehdot.

Jatkuvalle tiheysfunktiolle integraali lasketaan integroimalla tihysfunktiota koko määrittelyalueensa yli:

\[ \int_{-\infty}^{\infty} f \left( x \right) dx = 1 \]

Jos kyseessä olisi monen muuttujan tiheysfunktio, niin tällöin integrointi tehtäisiin kaikkien muuttujien määrittelyalueiden yli.

Esimerkkejä yhden muuttujan jatkuvista tiheysfunktioista

Jatkuvan tasajakauman tiheysfunktio on:

\[\begin{split} \begin{equation} f \left( x \right) = \begin{cases} \frac{1}{b-a}, & \text{jos } a\leq x \leq b \\ 0, & \text{muutoin} \end{cases} \end{equation} \end{split}\]

jossa arvon \(x\) likelihood-arvo \(f\left( x \right)\) on siis vakio välillä \(a\):sta \(b\):hen ja nolla muutoin. Kahden pisteen likelihood-arvojen osamäärä kuvaa näiden pisteiden suhteellista esiintymistodennäköisyyttä. Seuraavassa kuvassa on esitetty esimerkki jatkuvasta tasajakautuneesta todennäköisyystiheysfunktiosta.

Fig. 11 Esimerkki tasajakaantuneesta todennäköisyystiheysfunktiosta, joka saa nollasta poikkeavia arvoja välillä 0…5. Viivan alle jäävän alueen pinta-ala on yksi.

Tasajakauman parametrit \(a\) ja \(b\) pitää olla etukäteen tiedossa, että tiheysfunktion arvot saa laskettua.

Jos tarkastellaan \(\Delta x\):n levyistä aluetta mistä kohtaa tahansa välillä \([a,b]\), niin tämän alueen pinta-ala pysyy vakiona ja tällöin myös todennäköisyys mille tahansa \(x\):n arvoille välillä \([a,b]\) on vakio. Toisin sanoen tasajakaumassa kaikki arvot välillä \([a,b]\) ovat yhtä todennäköisiä, minkä näkee myös siitä, että eri kohdasta laskettujen likelihood-arvojen osamäärä on vakio.

Seuraavassa kuvassa on esimerkki jatkuvasta ja symmetrisestä kolmiojaukautuneesta todennäköisyystiheysfunktiosta.

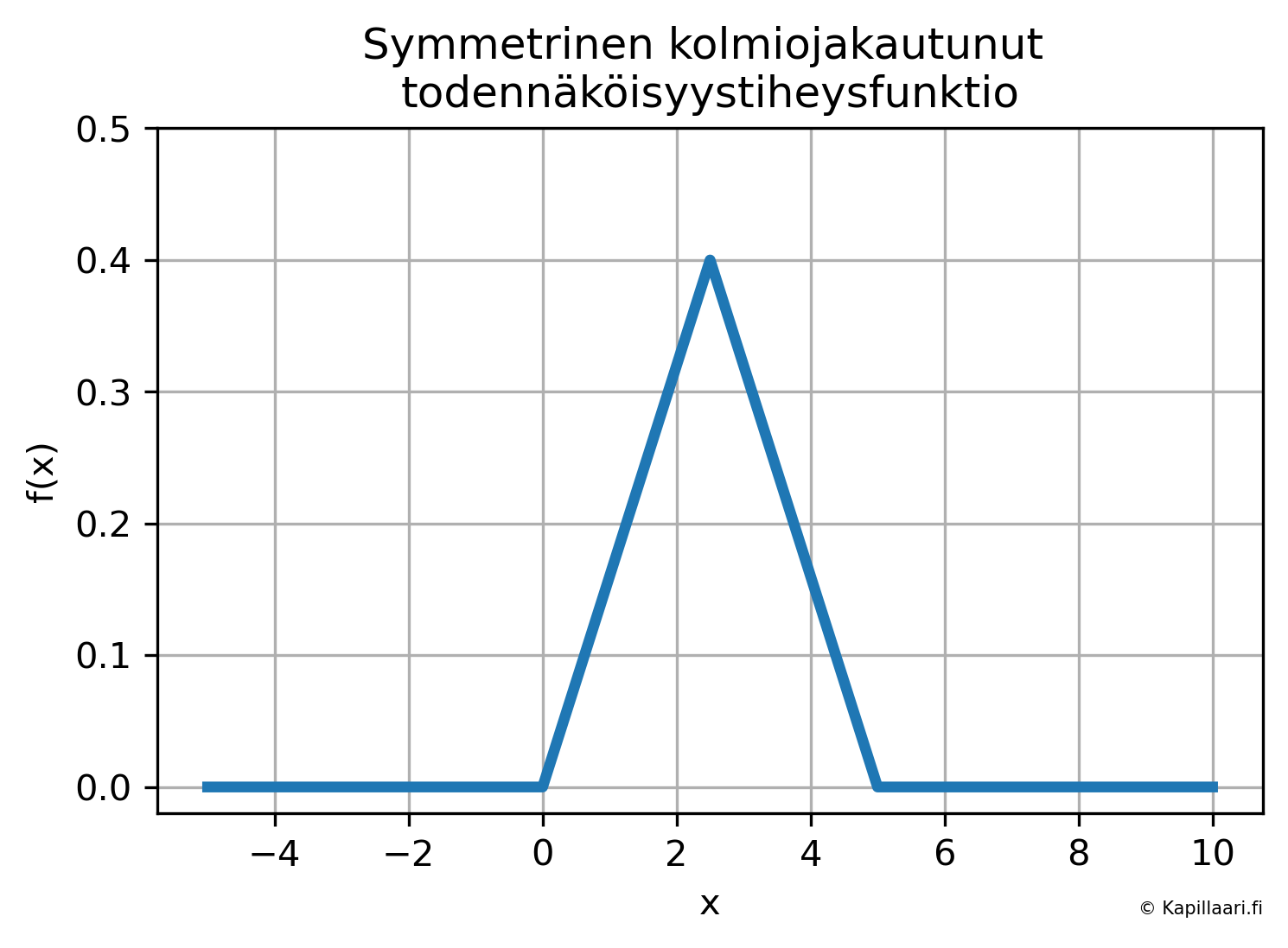
Fig. 12 Esimerkki symmetrisestä kolmiojakautuneesta todennäköisyystiheysfunktiosta. Funktio saa nollasta poikkeavia arvoja samoilla muuttujan \(x\) arvoilla kuin edellä tasajakaumassa, mutta nyt arvot lähellä alueen keskikohtaa ovat todennäköisempiä, kuin arvot alueen reunoilla. Viivan alle jäävän alueen pinta-ala on yksi.

Kolmiojakauman keskikohdan arvot ovat kaksi kertaa niin todennäköisiä, kuin tasajakauman keskikohdan arvot. Jos satunnaismuuttujan arvojen jakaumasta on olemassa tällaista tietoa, niin sitä voi pyrkiä ottamaan laskelmissa huomioon käyttämällä mahdollisimman sopivaa todennäköisyysjakaumaa.

Normaalijakauman tiheysfunktio on:

\[ f \left( x \right) = \frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right) ^2} \]

Funktiota kutsutaan myös Gaussin kellokäyräksi, tosin nykyään kellot muistuttavat ehkä kirkonkellojen sijaan enemmänkin tasajakauman näköisiä digitaalinäyttöjä. Kaavan alussa oleva kerroin tekee sen, että tiheysfunktion integraali menee ykköseksi.

Arvoa \(x\) vastaava likelihood-arvo \(f(x)\) on kaikkein suurin lähellä muuttujan \(X\) odotusarvoa \(\mu\). Esimerkki normaalijakaumasta (eli normaalijakautuneesta todennäköisyystiheysfunktiosta) on esitetty seuraavassa kuvassa.

Fig. 13 Esimerkki normaalijakautuneesta todennäköisyystiheysfunktiosta. Jakauman keskiarvo on kohdassa \(a + (b-a)/2 = 2,5\) ja keskihajontana on käytetty arvoa \((b-a)/4 = 1,25\). Viivan alle jäävän alueen pinta-ala on yksi.

Varsinaiset todennäköisyydet saadaan edellä olleen jatkuvan tasajakauman tapaan normaalijakautunutta tiheysfunktiota integroimalla. Tällöin jos tarkastellaan vakiosuuruista, \(\Delta x\):n levyistä aluetta, niin tämän alueen pinta-ala on suurimmillaan lähellä odotusarvoa \(\mu\). Näin ollen likelihood-arvojen lisäksi myös todennäköisyyksiä tarkastelemalla \(x\) saa todennäköisimmin arvoja odotusarvon läheltä. Parametri \(\sigma\) kuvaa sitä, että kuinka laajalle alueelle \(X\):arvot levittäytyvät odotusarvosta \(\mu\) katsoen. Suureiden \(\mu\) ja \(\sigma\) määritelmiä katsotaan tarkemmin myöhemmin tässä tekstissä.

Jos joidenkin tiettyjen tapahtumien toteutuneet lukumäärät esitetään histogrammina ja näihin arvoihin sovitetaan normaalijakauma, niin näin saatu käyrä ei vielä ole todennäköisyystiheysfunktio. Tiheysfunktiota varten näin saatua regressiokäyrää tulee vielä skaalata siten, että käyrän alle jääväksi pinta-alaksi tulee yksi. Tässä kohtaa on kuitenkin hyvä huomata, että aina ei tarvitava täyttä todennäköisyystiheysfunktiota, vaan joskus (esimerkiksi Bayesiläisissä tarkasteluissa) riittää saada käyrän pelkkä vaakasuuntainen sijainti kohdalleen.

Kertymäfunktiot

Kertymäfunktio on histogrammien ohella näppärä työkalu esimerkiksi datajoukkon tilastollisten ominaisuuksien arviointiin. Kertymäfunktion määritelmä on:

\[ F(x) = P(X \leq x) \]

eli kertymäfunktio tietyssä pisteessä tarkoittaa sitä todennäköisyyttä, että satunnaismuuttuja \(X\) saa enintään \(x\):n suuruisia arvoja. Diskreetille tapaukselle kertymäfunktio on:

\[ F(x) = P(X \leq x) = \sum_{x_i \leq x} f(x_i) \]

Tällöin siis summataan yhteen kaikki diskreetit pistetodennäköisyydet \(f(x_i)\), joille pätee, että \(x_i\) on pienempi tai yhtä suuri kuin \(x\), joka annetaan laskentakaavalle argumenttina.

Jatkuvalle tapaukselle kertymäfunktio on:

\[ F(x) = P(X \leq x) = \int_{-\infty}^{x} f(x) dx \]

Tässä kohtaa voi olla hyödyllistä huomata, että kertymäfunktion laatimiseksi \(X\):n tulee olla sellainen, että sen toteutuneet arvot \(x\) on mielekästä laittaa suuruusjärjestykseen. Koska tiheysfunktion pinta-alan tulee olla yksi (1), niin tiheysfunktiosta integroitu kertymäfunktio saa siis arvoja nollasta ykköseen.

Usean muuttujan jakaumat

Useimmiten asiat riippuvat useista eri tekijöitä ja todennäköisyystiheysfunktioissa tämä tarkoittaa monen muuttujan tiheysfunktioiden käyttämistä (yhteisjakauma, joint probability distribution). Tällaisessa tilanteessa tiheysfunktio saa siis argumenttina useita arvoja \( x_1, x_2, ..., x_n \), joiden perusteella funktiosta saadaan laskettua diskreetin tapauksen pistetodennäköisyys tai jatkuvan tapauksen likelihood-arvo.

Yksi usean muuttujan todennäköisyystiheysfunktioihin liittyvä asian on muuttujien riippumattomuus: Tiheysfunktion argumentit saattavat korreloida keskenään, eli suureen \(x_1\) tunteminen antaa tietoa myös suureesta \(x_2\). Jos taas eri muuttujat eivät korreloi keskenään, niin tällöin niiden sanotaan olevan riippumattomia, ja yhden muuttujan arvon tunteminen ei anna lisätietoa toisen muuttujan arvosta. Muuttujien keskinäinen riippumattomuus on tärkeä erikoistapaus, josta seuraa se, usean muuttujan yhteisjakauma saadaan kyseisten tulona:

\[ f(x, y) = f_X(x) \cdot f_Y(y) \]

Jos tämä ehto ei täyty, niin riippuvuussuhde voi olla lineaarinen tai tätä monimutkaisempi. Kahden muuttujan välisen lineaarisen riippuvuuden olemassa oloa voi tutkia esimerkisi Pearsonin tulomomenttikorrelaatiokertoimen \(\rho\) tai Spearmanin järjestyskorrelaatiokertoimen \(r\) avulla. Näistä jälkimmäisen käyttöä kannattaa pohtia silloin, jos korrelaation muoto ei ole tiedossa.

Odotusarvo

Odotusarvo voi olla ennestään tuttu esimerkiksi vedonlyönnistä, jossa yksittäisen pelin voi ajatella olevan ainakin matemaattisesti kannattava, jos pelin odotusarvo jää pelaajan kannalta positiiviseksi. Esimerkiksi, jos 10 euron panoksella on mahdollisuus voittaa 20 euroa 25 % todennäköisyydellä, niin pelin odotusarvo on tällöin: (-10 eur * 1,0) + (20 eur * 0,25 + 0 eur * 0,75) = (-10 eur) + (5 eur + 0 eur) = -5 eur, eli pelin odotusarvo on negatiivinen, eikä peliin kannata osallistua. Tällöin siis sijoittamansa panoksen menettää 100 %:n varmuudella ja 20 euron voiton saa 25 %:n todennäköisyydella. Voiton todennäköisyyden tulisi olla yli 50 %, jotta peliin edes periaatteessa kannattaisi lähteä.

Odotusarvo \(E(X)\) määritellään diskreetin muuttujan \(X\) tapauksessa seuraavasti:

\[ \mu = E(X) = \sum_{i=1}^{n} x_i \cdot f(x_i) \]

jossa indeksi \(i\) käy läpi muuttujan \(X\) toteutuneet arvot ja pistedennäköisyysfunktion \(f\) arvot pisteissä \(x_i\). Jatkuvan satunnaismuuttujan odotusarvo lasketaan seuraavasti:

\[ \mu = E(X) = \int_{-\infty}^{\infty} x f(x) dx \]

Odotusarvo-operaattorin avulla voidaan tehdä tiettyjä laskutoimituksia ja näin on johdettu mielenkiintoisia tuloksia myöhempää käyttöä varten.

Ensimmäinen mielenkiintoinen tulos liittyy tilanteeseen, jossa odotusarvo lasketaan satunnaismuuttujasta \(X\) riippuvalle funktiolle \(g(X)\) (Law of the unconscious statistician). Odotusarvon laskelmiseksi ei ole pakko määrittää tulosarvojen täyttä jakaumaa, vaan riittää tietää ainoastaan satunnaismuuttujan \(X\) jakauma. Eli toisin sanoen:

\[ E\left( g\left( X \right) \right) = \int_{-\infty}^{\infty} g(x) f_X(x) dx \]

Funktio \(f_X(x)\) tarkoittaa muuttujan \(X\) todennäköisyystiheysfunktiota.

Toinen kätevä seikka on, että odotusarvo on lineaarinen (linearity of expectation, Grinstead & Snell, Ch. 6), eli vakiolla kertominen voidaan ottaa odotusarvon eteen ja summan odotusarvo laskea odotusarvojen summana:

\[\begin{split} \begin{align} E(\alpha X + \beta Y) \\ =& \int_{\Omega} (\alpha x + \beta y) f_\Omega(x,y) d\Omega \\ =& \int_X \int_Y (\alpha x + \beta y)f_{X,Y}(x,y) dx dy \\ =& \int_X \int_Y \alpha x f_{X,Y}(x,y) dx dy \\ &+ \int_X \int_Y \beta y f_{X,Y}(x,y) dx dy \\ =& \alpha \int_X x \left( \int_Y f_{X,Y}(x,y) \right) dx \\ &+ \beta \int_Y y \left( \int_X f_{X,Y}(x,y) \right) dy \\ =& \alpha \int_X x f_X(x) dx + \beta \int_Y y f_Y(y) dy \\ =& \alpha E(X) + \beta E(Y) \end{align} \end{split}\]

Tämä pitää paikkansa, vaikka muuttujat \(X\) ja \(Y\) olisivat toisistaan riippuvia. Mahtavaa!

Varianssi

Varianssin määritelmä ja ominaisuuksia

Varianssi on satunnaismuuttujan poikkeamien neliöiden odotusarvo, kun poikkeamat määritellään satunnaismuutujan arvojen erotuksena odotusarvostaan. Hyödyntämällä edellisen luvun oppeja odotusarvoista, saadaan:

\[ \sigma^2 = V(X) = E((X - E(X))^2) = E((X - \mu)^2) \]

Jos satunnaismuuttujaan lisätään vakio, niin tämä ei muuta varianssin arvoa:

\[\begin{split} \begin{align} V(X+c) \\ =& E( ((X+c) - E(X+c))^2 ) \\ =& E( ((X+c)-(\mu+c))^2 ) \\ =& E( (X+c - \mu - c)^2 ) \\ =& E( (X-\mu)^2 ) \\ =& V(X) \end{align} \end{split}\]

Sen sijaan, jos muuttuja kerrotaan vakiolla \(c\), niin tämä vastaa varianssin kertomista vakion neliöllä:

\[\begin{split} \begin{align} V(cX) \\ =& E((cX - E(cX))^2) \\ =& E(( cX - cE(X) )^2) \\ =& E( c^2(X-E(X))^2 ) \\ =& c^2 E( (X-E(X))^2 ) \\ =& c^2 V(X) \end{align} \end{split}\]

Satunnaismuuttujien summan varianssi on varianssien summa, plus muuttujien kovarianssista seuraava yhteisvaikutustermi. Tämän todistamiseksi kirjoitetaan ensin summa näkyviin varianssin määritelmän sisään:

\[\begin{split} \begin{align} V(X+Y) \\ =& E( ((X+Y)-E(X+Y))^2 ) \\ =& E( (X+Y-\mu_X - \mu_Y)^2 ) \\ =& E( (X-\mu_X + Y - \mu_Y)^2 ) \end{align} \end{split}\]

…kirjoitetaan tämän jälkeen neliöön korottaminen auki:

\[\begin{split} \begin{align} V(X+Y) \\ =& E(XX-X\mu_X+XY-X\mu_Y \\ &- \mu_X X + \mu_X^2 - \mu_X Y + \mu_X \mu_Y \\ &+ YX -Y\mu_X + Y^2 - Y\mu_Y \\ &- \mu_Y X + \mu_Y \mu_X - \mu_Y Y + \mu_Y^2) \end{align} \end{split}\]

Järjestellään termejä ja mennään lopuksi määritelmiä takaisin päin:

\[\begin{split} \begin{align} V(X+Y) \\ =& E(XX - X\mu_X - \mu_X X + \mu_X^2) \\ +& E(Y^2 - Y\mu_Y - \mu_Y Y + \mu_Y^2) \\ +& E(XY - X\mu_Y \mu_X Y + \mu_X \mu_Y) \\ +& E(YX - \mu_Y X -Y \mu_X + \mu_Y \mu_X) \end{align} \end{split}\]

\[\begin{split} \begin{align} V(X+Y) \\ =& E((X-\mu_X)^2) \\ +& E((Y-\mu_Y)^2) \\ +& 2 E((X-\mu_X)(Y-\mu_Y)) \end{align} \end{split}\]

\[ V(X+Y) = V(X) + V(Y)+ 2 Cov(X,Y) \]

Viimeisessä vaiheessa on käytetty kovarianssin määritelmää:

\[ Cov(X,Y) = E((X-\mu_X)(Y-\mu_Y)) \]

Jos kovarianssi on nolla, niin tällöin jäljelle jää:

\[ V(X+Y) = V(X) + V(Y) \]

Eli toisistaan riippumattomien satunnaismuuttujien summan varianssi on varianssien summa. Tätä tietoa hyödynnetään myöhemmin laskettaessa mittausepävarmuuden yhdistettyä varianssia.

Otoskeskiarvo ja sen keskihajonta

Tähän mennessä ollaan päästy satunnaismuuttujista niiden jakaumafunktioihin, jakaumista edelleen odotusarvoihin ja odotusarvoista varianssiin. Näiden avulla päästään käsiksi otoksen keskiarvoon ja keskiarvon keskihajontaan, joita tarvitaan myöhemmin mittausepävarmuuden määrittelemisessä.

Ajatellaan tilannetta, jossa meillä on otoksen verran arvoja suureesta \(X\). Lasketaan näiden odotusarvo olettamalla jokainen mittaustulos keskenään yhtä todennäköiseksi (\(f(x_i) = 1 / n\)). Näin saatavan tuloksen huomataan vastaavan otoskeskiarvoa:

\[ E(x_i) = \sum_{i=1}^{n} x_i \frac{1}{n} = \frac{1}{n} \sum_{i=1}^n x_i = \bar{x} \]

Suurten lukujen lain mukaan otoskeskiarvo on samalla populaation keskiarvon harhaton estimaattori. Harhattomuuden lisäksi voidaan populaation keskiarvoestimaattorilta toivoa myös muita ominaisuuksia, kuten pientä varianssia. Tätä varten voi olla perusteltua käyttää otoskeskiarvon sijaan esimerkiksi trimmattua (trimmed) keskiarvoa tai otoksen mediaania.

Otoksen varianssi on edellä kuvatuilla kaavoilla laskettuna on poikkeamien neliöiden keskiarvo:

\[ V(x_i) = \sum_{i=1}^n (x_i-\bar{x})^2 \frac{1}{n} = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2 = s_n^2(x_i) \]

Tällä tavalla saatu estimaattori \(s_n^2\) on kuitenkin harhainen (biased), eli vaikka otoksen kokoa kasvatettaisiin rajatta, niin otosvarianssi poikkeaisi todellisesta populaation varianssista. Populaation varianssin harhaton estimaattori saadaan korjaamalla harhaista otosvarianssia kertoimella \(n/(n-1)\) (Bessel’s correction), jolloin saadaan:

\[ s^2(x_i) = \frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2 \]

Korjaustermin voi itse asiassa valita muillakin tavoilla ja näillä valinnoilla on jonkin verran vaikutusta erityisesti silloin, kun otoskoko on pieni. Arvon \(n-1\) käyttö on kuitenkin esitetty GUM-oppaassa (JCGM 100:2008, luku 4.2), joten käytetään sitä.

Mittausepävarmuuksien määrittämistä varten tarvitaan vielä yksi varianssi lisää, eli otos_keskiarvon_ vaihtelua kuvaava varianssi. Se saadaan laskettua harhattomasta otosvarianssista jakamalla se otoksen koolla:

\[ s^2(\bar{x}) = \frac{s^2(x_i)}{n} \]

Tämä on mielenkiintoinen juttu, että otoskeskiarvon varianssi saadaan näin helposti otoksen varianssista, mistä se johtuu? Lausekkeen todistus löytyy esimerkiksi täältä ja se perustuu siihen, että keskiarvon lausekkeessa on mukana \(n\) kappaletta mittaustuloksia:

\[\begin{split} \begin{align} V(\bar{X}) \\ =& V \left( \frac{X_1 + X_i + \cdots + X_n}{n} \right) \\ =& \left( \frac{1}{n} \right)^2 \left( V(X_1) + V(X_2) + \cdots + V(X_n) \right) \\ =& \left( \frac{1}{n} \right)^2 (\sigma^2 + \sigma^2 + \cdots + \sigma^2) \\ =& \frac{\sigma^2}{n} \end{align} \end{split}\]

Todistuksen alussa otoskeskiarvo on korvattu määritelmällään ja sen jälkeen vakiokerroin \(1/n\) on otettu varianssin eteen kertoimeksi (ks. kaavat aikaisemmin). Otoksen jokaiseen mittauspisteen ajatellaan liittyvän samaan todennäköisyysjakaumaan, jossa varianssa \(\sigma^2\) (tai harhaton otosvarianssi \(s^2\)) on siis sama kaikille jakaumasta poimittaville arvoille.

Ottamalla otoskeskiarvon varianssista neliöjuuri, saadaan otoskeskiarvon keskihajonta:

\[ s(\bar{x}) = \sqrt{\frac{s^2(x_i)}{n}} \]

GUM-oppaan kannalta tämä on havaintoaineiston tilastolliseen käsittelyyn perustuva standardiepävarmuus \(u\):

\[ u(x) = s(\bar{x}) \]

Epävarmuus voidaan ilmoittaa myös suhteellisena epävarmuutena, joka on standardiepävarmuus jaettuna suureen arvolla, eli:

\[ \frac{u(x)}{| \bar{x} | } \]

Suhteellinen epävarmuus on dimensioton luku, joka on suuruudeltaan positiivinen tai nolla. Suhteellisen epävarmuuden laskenta toimii parhaiten silloin, kun suureen arvo on riittävän kaukana nollasta.

Muista tiedoista johdettu standardiepävarmuus

Aina kaikista suureista ei ole saatavilla mittausdataa otoskeskiarvon ja standardiepävarmuuden laskentaa varten. Jotta myös tällaiset epävarmuuslähteet saadaan laskentaan mukaan, tulee niille käyttää muita menetelmiä. Käytännössä tämä voi tarkoittaa esimerkiksi tiedon etsimistä valmistajien ohjeista, kalibrointitodistuksista ja tieteellisestä kirjallisuudesta.

Yksi mahdollinen tapa määrittää standardiepävarmuuksia on määrittää satunnaismuuttujan todennäköisyystiheysfunktio kirjallisuuteen ja asiantuntija-arvioon perustuen. Tällöin valitaan ensin todennäköisyysjakauman tyyppi ja tämän jälkeen asetetaan sen parametrit siten, että jakauma kuvastaa parasta käytössä olevaa tietoa kyseisestä satunnaismuuttujasta. Tämän jälkeen jakaumalle voidaan laskea sen varianssi ja edelleen keskihajonta, jotka kuvaavat nyt kyseisen muuttujan standardiepävarmuutta. Tekstin alussa oli esillä esimerkit tasajakaumasta, kolmiojakaumasta ja normaalijakaumasta, mutta samaa ideaa voi käyttää mille tahansa jakaumalle. Jakauman määrittämisen yksi etu on se, että kuvaajien piirtäminen on havainnollinen tapa pelkkien lukuarvojen käsittelyyn verrattuna ja kuvaajat mahdollistavat myös epävarmuuksista keskustelemisen muiden asiantuntijoiden kanssa.

GUM-ohjeessa on annettu analyyttisia ratkaisuja edellä mainittujen perustapausten varianssien laskemiseksi, joita käydään seuraavassa lyhyesti läpi.

Jos tiheysfunktioksi asetetaan kaikki realistisesti esiintyvät arvot kattava tasajakauma, jonka puolikas leveys on: \(a = (a_+ - a_-) / 2\), niin tällöin standardiepävarmuus on: \(u(x) = a / \sqrt{3} \approx 0,577a\).

Jos tiheysfunktioksi asetetaan kolmiojakauma siten, että tasakylkisen kolmion huippu on odotusarvon kohdalla ja kolmion puolikas leveys on: \(a = (a_+ - a_-) / 2\), niin tällöin standardiepävarmuus on: \(u(x) = a/\sqrt{6} \approx 0,408a\).

Jos tiheysfunktio voidaan olettaa normaalijakautuneeksi, niin tällöin välillä: \(\mu \pm 0,675\sigma\) on noin 50 % arvoista. Laskemalla tämän alueen leveyttä kuvaava suure: \(a = (a_+ - a_-) / 2\), saadaan standardiepävarmuudeksi: \(u(x) = (1/0,675)a = 1,48a\). Jos rajat asetetaan 2/3 (67 %) todennäköisyyden mukaan, niin tällöin voitaisiin käyttää suoraan arvoa: \(u(x) = a\). Tämä ei vastaa normaalijakauman todennäköisyyttä 2/3 tarkalleen, mutta pienen eron huomioon ottamista tällaisissa kertoimissa ei yleensä tehdä.

Tilastollisen datan analysoimisen avulla määritettyä standardiepävarmuutta kutsutaan GUM-oppaassa tyypin A standardiepävarmuudeksi (type A standard uncertainty). Muihin menetelmiin perustuvaa standardiepävarmuutta nimitetään tyypin B standardiepävarmuudeksi. GUM-oppaan liitteessä E.4 tuodaan esille, että tyypin B standardiepävarmuudet eivät kuitenkaan välttämättä ole sen huonompia verrattuna tyypin A arvoihin, koska erityisesti pienten otosten tapauksessa mittausdatasta määritetyt standardiepävarmuudet voivat itsessään olla huomattavan epävarmoja (JCGM 100:2008, liite E.4).

Taylorin sarja

Mittausepävarmuuden määrittämisen ns. peruspakettia varten tarvitaan vielä yksi työkalu pakkiin: Taylorin sarja, jonka ideana on approksimoida tarkasteltavaa funktiota kehityspisteen välittömässä läheisyydessä. Taylorin sarjakehitelmä \(f(x)\) pisteen \(a\) ympäristössä on:

\[ f(x) = f(a) + \frac{f'(a)}{1!}(x-a) + \frac{f''(a)}{2!} (x-a)^2 + \cdots \]

Mitä lähempänä muuttuja \(x\) on kehityspistettä \(a\), sitä tarkempia tuloksia Taylorin sarjakehitelmä antaa. Usein riittävään tarkkuuteen päästään käyttämällä vain ensimmäisen derivaatan termejä. Pudottamalla korkeamman asteen termit sarjakehitelmästä pois ja siirtämällä termejä saadaan:

\[ \Delta y = f(x) - f(a) = \frac{f'(a)}{1!} (x-a) \]

Tällä tavoin saadaan siis tietoa siitä, että kuinka suuria muutoksia lähtösuureen \(x\) pienet muutokset aiheuttavat tulossuureeseen \(y\). Tätä samaa asiaa olisi mahdollista tutkia myös esimerkiksi Monte Carlo -menetelmällä, mutta ei käsitellä sitä sen tarkemmin tässä.

Lähtösuureiden keskinäisiä riippuvuuksia ei tässä käsitellä, vaan kaikki lähtösuureet on oletettu toisistaan riippumattomiksi. Yleisesti ottaen eri suureiden välillä voi esiintyä korrelaatiota ja nämäkin tilanteet olisi hyvä pystyä tunnistamaan ja huomioimaan. Taylorin sarjan näkökulmasta tämä tarkoittaisi usean muuttujan sarjakehitelmän käyttämistä, jossa olisi mukana myös korkeamman asteen osittaisderivaatat usean muuttujan suhteen.

Epävarmuuksien yhdistäminen

Yhdistetty standardiepävarmuus

Tarkasteltavalle suureelle ilmoitettava mittausepävarmuus on GUM-oppaan kannalta niin kutsuttu yhdistetty standardiepävarmuus (combined standard uncertainty). Tätä tavoitetta ajatellen GUM-opas lähtee liikkeelle siitä, että meillä on jokin tarkasteltavan suureen \(Y\) kuvaava funktio \(f(\dots)\), eli:

\[ Y = f(X_1, X_2, \dots, X_n) \]

Lähtösuureet \(X_1, X_2, \dots\) voivat edelleen riippua muista suureista omien funktioidensa kautta, jolloin tarkasteltavan suureen \(Y\) taustalla voi olla laajakin analyysi erilaisista tekijöistä. Toisaalta tarkastavan suureen kuvaava funktio voi olla hyvin yksinkertainenkin, esimerkiksi \(Y = X\) silloin, kun vaikkapa luetaan lämpötilan mittaustulos suoraan nestelämpötilamittarin asteikolta.

Tarkasteltavaan suureeseen \(Y\) liittyvä yhdistetty varianssi lasketaan seuraavasti:

\[ u_c^2(y) = \sum_{i=1}^n \left( \frac{\partial f}{\partial x_i} \right) ^2 u^2(x_i)\]

Funktio \(f\) on suureen \(y\) määrittävä funktio, \(\partial f / \partial x_i\) on funktion \(f\) osittaisderivaatta muuttujan \(x_i\) suhteen ja \(u^2(x_i)\) tarkoittaa suureeseen \(x_i\) liittyvän standardiepävarmuuden neliötä, eli varianssia. Kaavassa hyödynnetään aikaisemmin esillä ollut tietoa varianssien summaamisesta, eli että riippumattomien satunnaismuuttujien summan varianssi on varianssien summa. Yhdistetyn standardiepävarmuuden laskennan näkökulmasta katsottuna satunnaismuuttujat ovat nyt eri lähtösuureisiin liittyviä epävarmuuslähteitä, jotka saavat omien standardiepävarmuuksiensa mukaisia arvoja nollan molemmin puolin. Näiden yhteisvaikutus, eli tarkasteltavan suureen \(y\) yhdistetty varianssi \(u_c^2(y)\) voidaan laskea varianssien yhteenlaskukaavan avulla suoraan yksittäisten varianssien \(u^2(y_i)\) summana. Yksittäiset varianssit \(u^2(y_i)\) saadaan laskettua tuomalla standardiepävarmuudet \(u(x)\) funktion \(f\) läpi Taylorin sarjakehitelmän avulla ja korottamalla tämän jälkeen neliöön.

Jos tarkasteltava suure on kahden suureen erotus \(y = x_A - x_B\), niin tällöin funktion osittaisderivaatat \(\partial y / \partial x\) supistuvat ykkösiksi ja yhdistetty standardiepävarmuus saadaan ottamalla neliöjuuri lähtösuureiden varianssien summasta:

\[ u_c(y) = \sqrt{ u^2(x_A) + u^2(x_B) } \]

Tätä on hyödynnetty tekstin loppupuolella olevassa laskuesimerkissä.

Laajennettu mittausepävarmuus

GUM-oppaan yksi keskeinen tavoite on luoda yhteiset käytännöt mittausepävarmuuden laskemiselle ja ilmoittamiselle, jotta mittausepävarmuudet osattaisiin ottaa oikeassa suhteessa huomioon päätöksenteossa. Liian suureksi kuvitellut mittausepävarmuudet voivat aiheuttaa ylimääräisiä kustannuksia tarpeettomien investointien muodossa ja liian pieneksi kuvitellut mittausepävarmuudet voivat aiheittaa hankaluuksia toimimattomien laitteiden tai muiden järjestelmien kanssa. Suositeltavaksi käytännöksi on valikoitunut esittää mittausepävarmuudesta realistinen ja todennäköinen arvio standardiepävarmuuden muodossa, verrattuna esimerkiksi aikaisempiin käytäntöihin maksimiepävarmuuden ilmoittamisesta. (JCGM 100:2008, liite E)

Erinäisissä tilanteissa voidaan kuitenkin haluta tarkastella lukuarvoon liittyvän epävarmuuden ylärajaa, jota tarkoitusta varten on määritelty niin kutsuttu laajennettu mittausepävarmuus \(U\) (expanded uncertainty). Laajennetun mittausepävarmuuden määritelmä on:

\[ U = k u_c(y) \]

Kerroin \(k\) on kattavuuskerroin (coverage factor), jolle käytetään tyypillisesti arvoa 2 tai 3. Jos tilanteeseen vaikuttavat epävarmuuslähteet ovat normaalijakautuneita, niin edellä olevaa menettelyä käytettäessä standardiepävarmuus (\(k\) = 1) kattaa noin 68 % tarkasteltavan suureen vaihtelusta. Arvon \(k\) = 2 käyttäminen johtaa normaalijakautuneiden mittausepävarmuuksien tapauksessa noin 95 % luottamusväliin ja arvon \(k\) = 3 käyttäminen noin 99 % luottamusväliin. Näiden prosenttilukujen määrittämiseen liittyy kuitenkin kaikenlaisia kysymyksiä, joten tarkat prosenttiluvut ovat lähinnä suuntaa-antavia. Kertoimen \(k\) arvoja on mahdollista haarukoida tarkemmin esimerkiksi t-jakaumasta. (JCGM 100:2008, liite G)

Jos suureelle ilmoitetaan laajennettu mittausepävarmuus standardiepävarmuuden sijaan, niin tämä tulee ilmoittaa lukujen yhteydessä selvästi ja kertoa samalla myös käytetty kattavuuskerroin.

Kertoimen \(k\) käyttö tulee tehdä vasta aivan laskelmien lopuksi, eli kaikki välivaiheet lasketaan ilman minkäänlaisia kattavuuskertoimia. Tällöin säilytetään eteenpäin raportoitavien tulosten yhdenmukaisuus GUM-oppaan periaatteisiin nähden.

Laskentaesimerkki

Katsotaan laskuesimerkkinä betonisandwich-seinän U-arvoon liittyvää (mittaus)epävarmuutta, koska rakenne on Suomessa hyvin yleinen ja U-arvon laskeminen tämän kaltaiselle rakenteelle on yksi ensimmäisistä asioista, johon rakennusfysiikka opiskeltaessa yleensä törmätään. ”Mittaus”-sanan käyttö ei ehkä sovellu tähän yhteyteen kovin hyvin, koska laskuesimerkkiin ei liity U-arvon mittaamista, mutta pidetään tämä sana kuitenkin mukana sanaston pitämiseksi edes jossain määrin yhtenäisenä.

Tehdään heti lähtölauksesta monenlaisia yksinkertaistuksia. Oletetaan ainakin, että: 1) materiaalien lämmönjohtavuus on vakio, eli että lämpö- ja kosteusolosuhteet eivät vaikuta lämmönjohtavuuteen, 2) U-arvon laskentaan liittyvien suureiden välillä ei esiinny korrelaatioita, vaan kaikki suureet voidaan käsitellä toisistaan riippumattomina. ja 3) rakenteessa ei ole tuuletuskanavistoa, mekaanisia kiinnikkeitä, ilmarakoja, eristeen painumaa tai muita vastaavia asioita. Tavoitteena on siis laskea rakenteen U-arvoon liittyvä standardiepävarmuus, joka kattaisi rakenteen U-arvon vaihtelun tilanteessa, jossa U-arvo määritettäisiin samoissa olosuhteissa uudestaan ja uudestaan.

Yksiulotteisen, kerroksellisen rakenteen U-arvo saadaan kerrosten lämmönvastusten summan käänteislukuna:

\[ U = \frac{1}{R_{si} + R_{sk} + R_e + R_{uk} + R_{se}} \]

Muokataan hieman asettelua ja sijoitetaan lausekkeita:

\[\begin{split} U = \left( \left( h_{ci} + h_{ri} \right)^{-1} \\ + \frac{d_{sk}}{\lambda_{sk}} + \frac{d_e}{\lambda_e} + \frac{d_{uk}}{\lambda_{uk}} \\ + \left( h_{ce} + h_{re} \right)^{-1} \right)^{-1} \end{split}\]

…ja vielä lisää lämmönsiirtokertoimien osalta:

\[\begin{split} U = \left( \left( h_{ci} + (\varepsilon_i 4 \sigma T_{mi}^3) \right) ^{-1} \\ + \frac{d_{sk}}{\lambda_{sk}} + \frac{d_e}{\lambda_e} + \frac{d_{uk}}{\lambda_{uk}} \\ + \left( (4+4v) + (\varepsilon_e 4 \sigma T_{m3}^3) \right) ^{-1} \right)^{-1} \end{split}\]

Lausekkeessa on yhteensä 13 eri suuretta, joista 12 on tarpeen määrittää standardiepävarmuus. Stefan-Boltzmannin vakiossa standardiepävarmuutta ei ole (\(u(\sigma)\) = 0 W/(m2K4)), koska SI-järjestelmän päivityksen myötä tiettyjä suureita asetettiin vakioiksi ja Stefan-Boltzmannin vakio voidaan laskea suoraan näistä tarkoista arvoista.

Tässäkin mallissa on keskenään riippuvia suureita, sillä esimerkiksi elementin kokonaispaksuus sitoo yhteen sisä- ja ulkokuoren sekä lämmöneristekerroksen paksuudet, eli \(d_{sk} + d_{uk} + d_e = d_{kok}\). Näistä keskinäisiä riippuvuuksia ja niiden käsittelyä ei kuitenkaan ole juurikaan käsitelty tässä kirjoituksessa, joten ei oteta niitä huomioon tässäkään kohtaa.

Seuraavaan taulukkoon on koottu arviot lähtötietoihin liittyvistä standardiepävarmuuksista.

Table 3 U-arvolaskentaesimerkkiin liittyvien suureiden lukuarvot ja standardiepävarmuudet. Fysikaalisten ilmiöiden vaihtelusta aiheutuvia epävarmuuksia ei ole pyritty ottamaan näissä arvoissa huomioon, vaan tavoitteena on kuvata yksinkertaisen tilanteen toistettavuuteen liittyvä standardiepävarmuus.

Muuttuja	Suureen arvo	Standardiepävarmuus
\(h_{ci}\)	2,5 W/(m2K)	0,1 W/(m2K)
\(\varepsilon_i\)	0,9	0,03
\(\sigma\)	5,67 × 10-8 W/(m2K4)	0 W/(m2K4)
\(T_{mi}\)	294 K	0,3 K
\(d_{sk}\)	0,08 m	0,01 m
\(\lambda_{sk}\)	2,5 W/(mK)	0,05 W/(mK)
\(d_e\)	0,22 m	0,01 m
\(\lambda_e\)	0,038 W/(mK)	0,0005 W/(mK)
\(d_{uk}\)	0,07 m	0,01 m
\(\lambda_{uk}\)	2,5 W/(mK)	0,05 W/(mK)
\(v\)	3 m/s	0,3 m/s
\(\varepsilon_e\)	0,9	0,05
\(T_{me}\)	278 K	0,4 K

Jos sijoitetaan nämä lukuarvot yllä olevaan U-arvon laskentalausekkeeseen, saadaan rakenteen U-arvoksi 0,1659 W/(m2K) \(\approx\) 0,17 W/(m2K)

Seuraavaksi tarvitaan vielä osittaisderivaatat (herkkyyskertoimet) Taylorin sarjakehitelmää varten. Nämä saadaan edellä olevasta lausekkeesta derivoimalla. Osittaisderivaattojen analyyttisistä lausekkeista tulee hieman kirjoitettavaa, joten määritellään kirjoitustyön vähentämiseksi ja virheiden välttämiseksi seuraavat apusuureet:

\[ R = h_i^{-1} + \frac{d_{sk}}{\lambda_{sk}} + \frac{d_{e}}{\lambda_{e}} + \frac{d_{uk}}{\lambda_{uk}} + h_e^{-1} \]

\[ h_i = h_{ci} + \varepsilon_i 4 \sigma T_{mi}^3 \]

\[ h_e = 4 + 4 v + \varepsilon_e 4 \sigma T_{m3}^3 \]

Osittaisderivaattojen lausekkeet on koottu seuraavaan taulukkoon.

Table 4 U-arvolausekkeen osittaisderivaattojen analyyttiset lausekkeet sekä lähtötietojen mukaiset lukuarvot. (*) Kertoimet on annettu positiivisina, koska mittausepävarmuudet voivat vain kasvaa ja neliöön korottaminen tekee luvuista joka tapauksessa positiivisia.

Osittaisderivaatta	Lauseke	Lukuarvo (*)
\(\partial U / \partial h_{ci}\)	\(R^{-2} h_i^{-2}\)	0,000 47
\(\partial U / \partial \varepsilon_i\)	\(R^{-2} h_i^{-2} (4 \sigma T_{mi}^3)\)	0,002 68
\(\partial U / \partial T_{mi}\)	\(R^{-2} h_i^{-2} (12 \varepsilon_i \sigma T_{mi}^2)\)	0,000 02
\(\partial U / \partial d_{sk}\)	\(-R^{-2} \lambda_{sk}^{-1}\)	0,011
\(\partial U / \partial \lambda_{sk}\)	\(R^{-2} d_{sk} \lambda_{sk}^{-2}\)	0,000 35
\(\partial U / \partial d_e\)	\(-R^{-2} \lambda_e^{-1}\)	0,724
\(\partial U / \partial \lambda_e\)	\(R^{-2} d_e \lambda_e ^{-2}\)	4,192
\(\partial U / \partial d_{uk}\)	\(-R^{-2} \lambda_{uk}^{-1}\)	0,011
\(\partial U / \partial \lambda_{uk}\)	\(R^{-2} d_{uk} \lambda_{uk}^{-2}\)	0,000 31
\(\partial U / \partial v\)	\(4 R^{-2} h_e^{-2}\)	0,000 26
\(\partial U / \partial \varepsilon_e\)	\(R^{-2} h_e^{-2} (4 \sigma T_{me}^3)\)	0,000 32
\(\partial U / \partial T_{me}\)	\(R^{-2} h_e^{-2} (12 \varepsilon_e \sigma T_{me}^2)\)	3e-6

Yhdistämällä osittaisderivaattojen mukaiset herkkyyskertoimet ja edellä olleet standardiepävarmuudet GUM-oppaan mukaisesti, saadaan yhdistetyksi standardiepävarmuudeksi 0,007 54 W/(m2K).

Ehkä jossain määrin ennalta-arvattava, mutta laajuudeltaan yllättävä tulos luvuissa oli, että 92 % varianssista muodostui lämmöneristeen paksuuden mittausepävarmuudesta ja 8 % lämmöneristeen lämmönjohtavuuden mittausepävarmuudesta. Kaikkien loppujen suureiden vaikutus U-arvon mittausepävarmuuteen mahtui pyöristysvirheiden sisään. Mielenkiintoinen yksityiskohta laskelmissa oli, että suurin herkkyyskerroin (osittaisderivaatan lukuarvo) oli lämmöneristeen lämmönjohtavuudella, mutta suurin vaikutus rakenteen U-arvon epävarmuuteen tuli lämmöneristekerroksen paksuudesta. Edellä esitetyillä menetelmillä U-arvoksi saadaan siis 0,17 W/(m2K) ja tähän lukuun liittyväksi yhdistetyksi standardiepävarmuudeksi \(u_c\) = 0,01 W/(m2K).

U-arvon toistettavuuteen liittyvän epävarmuuden laajuutta voidaan havainnollistaa kasvattamalla rakenteen lämmöneristyskerroksen paksuutta, laskemalla uuden tilanteen U-arvo ja standardiepävarmuus, sekä katsomalla, että missä kohtaa U-arvojen erotus muuttuu tähän liittyvää standardiepävarmuutta tai laajennettua epävarmuutta suuremmaksi (kts. luku 5.5). Käytetään tässä esimerkin vuoksi kattavuuskerrointa \(k\) = 2. Eli kysymyksenä on, milloin \(\Delta U = U_2 - U_1 > k \cdot u_c(\Delta U)\)?

Kokeilemalla eri lämmöneristyskerroksen paksuuksia 10 mm porrastuksella, on U-arvojen erotus laajennetun epävarmuuden suuruinen (\(k\) = 2), kun uusi lämmöneristepaksuus on 250 mm. Tällöin siis lähtötilanteen U-arvo oli \(U_1\) = 0,166 W/(m2K), lopputilanteen U-arvo oli \(U_2\) = 0,147 W/(m2K), U-arvojen erotus oli \(\Delta U\) = -0,019 W/(m2K) ja laajennettu mittausepävarmuus \(U(\Delta U) = k \cdot u_c(\Delta U)\) = 0,019 W/(m2K).

Nyt tarkastellussa tilanteessa lämmöneristyspaksuuden tulisi muuttua siis vähintään 30 mm, jotta kahden eri rakenteen U-arvon välille olisi edes periaatteellisella tasolla löydettävissä tilastollisesti merkitsevä ero. Jos mukaan otettaisiin myös analyysistä pois jätetyt tekijät, niin tällöin tilastollisesti merkitsevän eron löytäminen edellyttäisi tätä suurempaa lämmöneristyspaksuuksien erotusta.

Yhteenveto

Yksinkertaisiinkin mittauksiin liittyy yleensä runsaasti erilaisia virhelähteitä ja näiden nimeäminen sekä käsittely on mahdollista tehdä monilla eri tavoilla. Yhtenäisten käytäntöjen edistämiseksi on laadittu GUM-opas, joka on mielenkiintoinen ja hyödyllinen julkaisu mittausepävarmuuksien laskennalliseen määrittämiseen ja ilmoittamiseen.

Tässä kirjoituksessa käytiin läpi eri suureiden lukuarvoihin liittyvien epävarmuuksien taustateoriaa ja GUM-oppaan mukaisia käytäntöjä mittausepävarmuuden määrittämiseen. Lisäksi käytiin läpi yksinkertaisen U-arvolaskentatapauksen tulokseen liittyvän standardiepävarmuuden laskenta ja se, että mitä nämä epävarmuudet tarkoittaisivat lämmöneristekerroksen paksuutena. Laskelma havainnollisti sitä, että kattavien epävarmuuslaskelmien tekeminen vaatii työtä ja huolellisuutta, mutta epävarmuuksien analysoiminen auttaa myös tunnistamaan probleemaan vaikuttavat tärkeimmät tekijät sekä erottelemaan tilastollisesti merkitsevät tulokset sattumasta.

Takaisin etusivulle