Todennäköisyyden määritelmiä ja rakenteiden arviointia

Todennäköisyyden määritelmiä ja rakenteiden arviointia#

Julkaistu alunperin 2021-07-25.

Todennäköisyydestä on olemassa useita tulkintoja, jotka kuitenkin kukin lisäävät omalla tavallaan ymmärrystä todennäköisyyteen liittyvien tilanteiden käsittelystä. Tässä kirjoituksessa käydään läpi ensin kolme yleisintä tulkintaa todennäköisyydestä. Tämän jälkeen ehdollisen todennäköisyyden määritelmää sovelletaan rakenneratkaisun puutteellisuuden arviointiin.

Todennäköisyyden määritelmiä#

Klassinen tulkinta#

Todennäköisyydelle on olemassa eri määritelmiä, mutta helpommista päästä ymmärrettävä on niin sanottu klassinen tulkinta: Meillä on \(N\) kappaletta vaihtoehtoja, jotka kaikki ajatellaan keskenään yhtä todennäköisiksi ja toisensa poissulkeviksi. Tällöin tapahtuman \(A\) todennäköisyys \(P(A)\) on \(A\):n esiintymiskertojen \(N_A\) suhde vaihtoehtojen kokonaismäärään \(N\), eli:

\[ P(A) = \frac{N_A}{N} \]

Tällöin voidaan esimerkiksi laskea, että ykkösen saamisen todennäköisyys noppaa heitettäessä on symmetrian perusteella yksi kuudesta, eli: P(A=”noppa antaa ykkösen”) = 1/6, mikä on noin 17 %.

Vastaavasti jos heitetään kahta noppaa, niin tällöin yhden heiton tulos voidaan esittää taulukon avulla seuraavasti:

Table 5 Kahta noppaa N1 ja N2 heittämällä saatavat noppien silmälukujen summat. Taulukossa on tummennettuna ne tapaukset, joissa noppien silmälukujen summa on vähintään 11. Tässä laskelmassa nopat eivät putoile pöydältä tai jää kulmalleen.#
		N2
		1	2	3	4	5	6
N1	1	2	3	4	5	6	7
	2	3	4	5	6	7	8
	3	4	5	6	7	8	9
	4	5	6	7	8	9	10
	5	6	7	8	9	10	11
	6	7	8	9	10	11	12

Kahta noppaa heitettäessä meillä on 6 \(\cdot\) 6 = 36 eri tilannevaihtoehtoa, jotka kaikki tunnetaan. Tällöin ykkösparin saamisen todennäköisyys on 1/36, eli noin 3 % (solu 1-1). Vastaavasti parin saamisen todennäköisyys on 6/36, eli noin 17 % (diagonaalin tapaukset). Edelleen todennäköisyys sille, että noppien silmälukujen summa on vähintään 11 on 3/36 = 8 % (lihavoidut solut oikeassa alakulmassa).

Klassisen todennäköisyyden määritelmän yksi hankaluus on siinä, että useinkaan mahdollisten lopputulosten lukumäärä ei pystytä laskemaan, minkä lisäksi eri tapahtumilla voi olla erilaiset todennäköisyydet tai ne voivat olla toisistaan riippuvia. Kuinka esimerkiksi laskea jonkin rakenneratkaisun vaatimustenmukaisuus, jos kaikkien toteutettujen rakenteiden lopputulemaa ei tunneta? Tähän kysymykseen voidaan pyrkiä pureutumaan frekventistisen tulkinnan avulla.

Frekventistinen tulkinta#

Frekventistisen tulkinnan mukaan:

\[\begin{split} \begin{align} p =& \lim_{n \rightarrow \infty} \frac{n_A}{n} \\ P(A) =& p \end{align} \end{split}\]

jossa \(P(A)\) on tapahtuman \(A\) todennäköisyys, \(p\) on raja-arvolausekkeesta saatu tulos ja \(n_A\) on tapahtuman \(A\) esiintymiskertojen lukumäärä \(n\):n suuruisessa otoksessa. Frekventistisen tulkinnan ytimessä on toistokoe, jossa tietty tilanne toistuu samanlaisena uudestaan ja uudestaan. Kun koetta on toistettu tarpeeksi monta kertaa, alkaa todennäköisyys \(p\) tasaantua lähelle jotakin tiettyä arvoa ja tämä asymptoottisesti lähestyttävä arvo katsotaan todennäköisyydeksi \(P(A)\).

Tehdään pythonilla laskelma, jossa heitetään yhtä noppaa uudestaan ja uudestaan ja kirjataan jokaisen heiton jälkeen talteen siihen mennessä kertynyt ykkössilmäluvun suhteellinen osuus \(p = n_A / n\). Seuraavassa kuvassa on esitetty 30 tällaisen laskelman tulos ensimmäiseltä 300 heitolta.

../../_images/frekventistinen_kapillaari_fi.png — Fig. 14 Simuloitu tulos nopanheitosta, jossa seurataan ykkösen saamisen todennäköisyyden määräytymistä heittojen määrän kasvaessa. Punaisella vaakaviivalla on esitetty klassisesta todennäköisyyden tulkinnasta laskettu ykkösen todennäköisyys 1/6 = 0,17. Simuloitujen todennäköisyyksien keskihajonta pienenee otoskoon kasvaessa.#

Kun otoskoko oli 300, niin 30 käyrän lopputulosten keskihajonta oli suuruusluokkaa 0,02 (variaatiokerroin noin 12 %), kun laskelmaa toisti useita kertoja. Jos variaatiokertoimen halusi olevan noin 5 % (0,0083/0,1667), niin heittoja tuli olla noin 2000 tai enemmän.

Kuvaa 14 katsomalla huomaa, että jos otoskoko olisi normaalijakaumaan liittyvän nyrkkisäännön > 30 mukainen, niin tällä olisi päästy osassa tapauksia oikeaan suuruusluokkaan, mutta epävarmuudet olisivat edelleen aika suuret. Riittävän otoskoon pohtimiseen ja valitsemiseen tulee siis käyttää riittävästi aikaa ja vaivaa, jotta tuloksiin jäävät epävarmuudet olisivat riittävän pienet suhteessa tarkkuustavoitteisiin.

Edelleen kuvasta 14 huomataan, että ykkösten määrä noppaa \(n\) kertaa heitettäessä on satunnaismuuttuja, joka saa eri arvoja koetta uusittaessa. Jos määritellään, että mahdollisia lopputuloksia on kaksi, jotka ovat: \(A\) = ”nopanheitosta tuli ykkönen” ja \(\bar{A}\) = ”nopanheitosta ei tullut ykkönen”, niin tällöin voidaan tapahtuman \(A\) esiintymiskertojen jakaumaa mallintaa binomijakaumalla (bi ~ kaksi).

Binomijakauman pistetodennäköisyysfunktio (diskreetti todennäköisyysjakauma) on:

\[ P \left( X = k \right) = \binom{n}{k} p^k \left( 1 - p \right) ^ {n-k} \]

jossa \(P(X = k)\) on tapahtuman \(X = k\) todennäköisyys, \(X\) on satunnaismuuttuja, \(n\) on toistojen kokonaismäärä, \(k\) on suotuisen tapahtuman toteutumisten lukumäärä, \(p\) on suotuisan tuloksen esiintymistodennäköisyys yleisesti ottaen ja \(\binom{n}{k}\) on binomikerroin, eli eri tapojen lukumäärä, joilla \(k\) alkiota voidaan valita \(n\):stä.

Ajatellaan tilannetta, että heitämme noppaa 100 kertaa. Ykkösten lukumäärän odotusarvo on: \(E(n_{X=1}) = P(X=1) \cdot n\) = (1/6) \(\cdot\) 100 \(\approx\) 17, mutta tuloksena saadaan 12 kpl ykkösiä. Kuinka todennäköinen tai epätodennäköinen tämä tulos oli? Asetetaan edellä olevaan binomijakauman lausekkeeseen \(n\) = 100 ja \(p\) = 1/6, jonka jälkeen laskelmat toistetaan eri suuruisille \(k\):n arvoille. Tällöin saadaan ykkösen eri esiintymismäärien todennäköisyyksille seuraava jakauma.

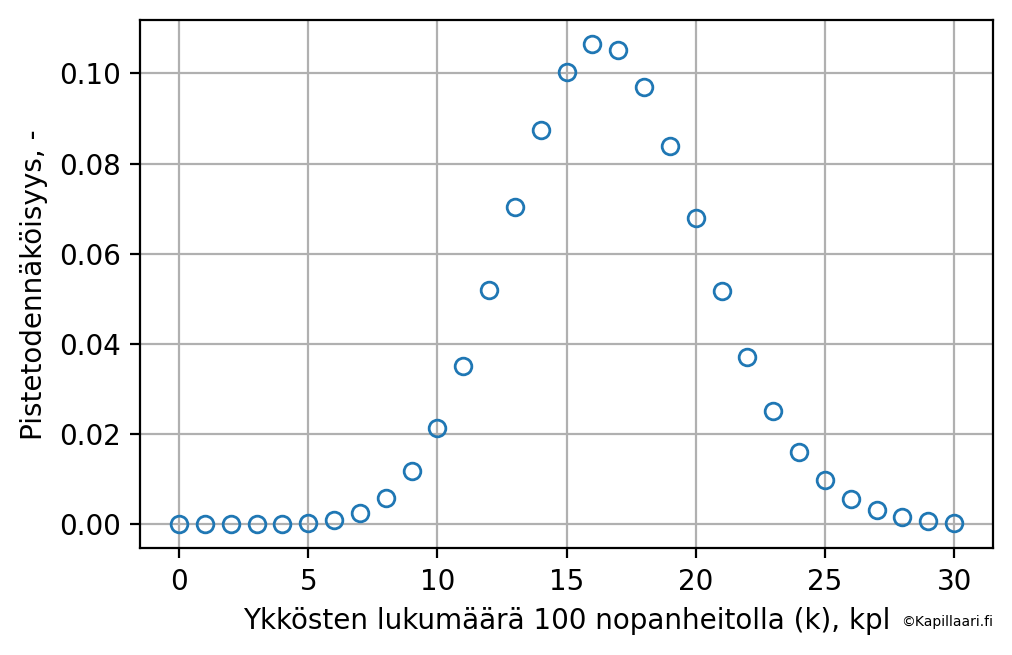
../../_images/binomijakauma_kapillaari_fi.png — Fig. 15 Binomijakauman pistetodennäköisyysfunktion kuvaaja, jossa on esitetty ykkösen esiintymiskertojen todennäköisyyksien jakauma heitettäessä noppaa 100 kertaa.#

Pistetodennäköisyyskuvaajasta ja numeroarvoisista tuloksista voidaan lukea, että tuloksen \(X\) = 12 tuloksen todennäköisyys on noin 5 %, kun taas kaikkein todennäköisimmän tuloksen \(X\) = 16 saamisen todennäköisyys on noin 10,7 %. Toisin sanoen, tuloksen \(X\) = 12 saamisen todennäköisyys on noin puolet kaikkein todennäköisimmän tuloksen todennäköisyydestä, eli hyvinkin mahdollinen tulos. Sitä kirjoittaja ei osaa tässä vaiheessa sanoa, että miksi binomijakauman huippu ei osu 17 ykkösen kohdalle, vaan tästä yhtä pienempään tulokseen.

Yksi tapa laskea binomijakaumasta luottamusvälit on yksinkertaisesti summata pistetodennäköisyyksiä yhteen jakauman huipun molemmilta puolilta. Jos tavoitellaan väliä, joka sisältää 95 % jakauman todennäköisyysmassasta, niin tällainen löytyy väliltä 9…23. Toisin sanoen jos 100 heiton tuloksena olisi saatu ≤ 8 tai ≥ 24 ykköstä, niin tällöin meillä olisi perusteet hylätä hypoteesi ykköstuloksiltaan tavanomaisesta nopasta (5 % kriittisyystasolla).

Nämä ovat sinällään aika mielenkiintoisia asioita, eli että jos meillä on taustalla vaikuttava prosessi, jonka osumatarkkuus on noin 17 %, niin meillä voi vielä 100 yksikön suuruisessa otoksessa olla aivan hyvin 9…23 osumaa, mikä tuntuu aika isolta hajonnalta otoksen kokoon nähden. Tämä kertoo siitä, että melko harvinaisista tai pienehköjen eroavaisuuksien ilmiöistä on vaikea saada luotettavaa tietoa ilman isoja otoskokoja.

Käsitellään tässä yhteydessä vielä kolmas todennäköisyyden tulkinta, eli Bayesiläinen tulkinta.

Bayesiläinen tulkinta#

Bayesiläinen todennäköisyyden tulkinta katsoo todennäköisyyttä subjektiivisena asiana, eli uskomuksen asteena (”degree of belief”). Baysiläiset todennäköisyyslaskelmat hyödyntävät vahvasti Bayesin lausetta:

\[ P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)} \]

jossa \(P(A | B)\) on tapahtuman \(A\) todennäköisyys ehdolla että (“|”) tapahtuma \(B\) on tosi, \(P(B | A)\) on tapahtuman \(B\) todennäköisyys ehdolla että \(A\) on tosi, \(P(A)\) on tapahtuman \(A\) a priori -todennäköisyys ja \(P(B)\) vastaavasti tapahtuman \(B\) a priori -todennäköisyys.

Todennäköisyys \(P(B)\) sisältää kaikki tapahtuman \(B\) ilmenemistilanteet, mukaan lukien sekä \(A\):n aiheuttamat (oikeat positiiviset), että muista systä johtuvat (väärät positiiviset). \(B\):n kaikki ilmenemismuodot (oikeat ja väärät positiiviset) kattava \(P(B)\) lasketaan kokonaistodennäköisyyden kaavalla (eng. law of total probability). Oletetaan tässä, että \(B\) voi tapahtua \(A\):n ollessa voimassa, tai sen komplementin \(\bar{A}\) ollessa voimassa. Kirjoitetaan tämä auki edellä olevaan kaavaan:

\[ P(A | B) = \frac{P(B | A) \cdot P(A)} { P(B|A) \cdot P(A) + P(B|\bar{A}) \cdot P(\bar{A}) } \]

Bayesin kaava on havainnollinen muun muassa tilanteissa, joissa puhutaan jostakin taustalla vaikuttavasta ilmiöstä \(A\) ja siitä saadusta mittaustuloksista \(B\). Tällöin kysymys on, että millä todennäköisyydellä ilmiö \(A\) on tosiaan käynnissä, jos kerran saimme mittauksistamme siihen viittaavan tuloksen B?

Koronavirusajalta yksi esimerkki voi koskea koronatestin tarkkuutta: Määritellään kaksi tapahtumaa: \(A\) = “minulla on korona” ja \(B\) = “testitulos oli positiivinen”. Tällöins siis saadaan: \(B|A\) = “minulla on korona ja tässä tilanteessa testi antoi positiivisen tuloksen” ja \(A|B\) = “testitulos oli positiivinen ja minulla todella on korona”. Vastaavasti saadaan: \(B|\bar{A}\) = “minulla ei ole koronaa, mutta mutta testi antoi silti positiivisen tuloksen”.

Sanotaan, että koronaviruksen esiintyvyys populaatiossa yleisesti ottaen on vaikkapa 5 %. Tämän perusteella saadaan: \(P(A)\) = 0,05 ja \(P(\bar{A}) = 1 - P(A) \) = 1 - 0,05 = 0,95. Nämä ovat niin sanottuja a priori -todennäköisyyksiä, joissa ei vielä ole mukana tapauskohtaisia mittauksia millään tavalla.

Lisäksi tarvitaan testin tarkkuus, eli kyky tunnistaa korona, kun henkilöllä on korona. Asetetaan: \(P(B|A)\) = 0,7.

Edelleen tarvitaan myös testin antamien positiivisten osuus, vaikka henkilöllä ei olisi koronaa. Tähän liittyen testeille annetaan usein prosenttiosuus oikein tunnistetuista negatiivista. Asetetaan: \(P(\bar{B} | \bar{A})\) = 0,99, eli kun henkilöllä ei ole koronaa, testitulos antaa negatiivisen tuloksen 99 %:ssa tapauksista. Tästä voidaan laskea: \(P(B|\bar{A}) = 1 - P(\bar{B}| \bar{A})\) = 1 - 0,99 = 0,01.

Jälkimmäisessä kaavassa on hyödynnetty komplementin määritelmää, jonka mukaan \(P(A) + P(\bar{A}) = 1\). Tämä ei muutu, vaikka sekä \(A\) että \(\bar{A}\) olisivat ehdollisia \(C\):stä, eli: \(P(A | C) + P(\bar{A} | C) = 1\).

Syöttämällä lukuarvot kaavaan, saadaan:

\[\begin{split} \begin{align} P(A | B) &= \frac{0,7 \cdot 0,05}{0,7\cdot0,05 + 0,01\cdot 0,95} \\ &= \frac{0,035}{0,035 + 0,0095} \\ &= 0,79 \end{align} \end{split}\]

Eli tuloksen perusteella meillä olisi 79 % prosentin todennäköisyydellä korona, kun saimme testistä positiivisen tuloksen. Jos todennäköisyyttä halutaan vielä kasvattaa, niin tällöin on mahdollista tehdä uusi testi samalle henkilölle.

Testi saisi kuitenkin olla eri testi ensimmäiseen nähden, koska jos ensimmäinen testi antoi väärän positiivisen jostain muusta syystä kuin sattumasta, niin tällöin kakkostestikin saattaisi näin tehdä. Laskuesimerkkiä varten kuitenkin oletetaan, että testien ominaisuuksia kuvaavat prosenttiluvut pysyvät samoina. Tällöin saadaan:

\[\begin{split} \begin{align} P(A | B) &= \frac{0,7 \cdot 0,79}{0,7\cdot 0,79 + 0,01\cdot 0,21} \\ &= \frac{0,55}{0,55 + 0,002} \\ &= 0,996 \end{align} \end{split}\]

Riippumattoman kakkostestin antaman positiivisen näytteen jälkeen on lähes varmaa, että henkilöllä on korona.

Bayesiläisessä tilastomatematiikassa on paljon erilaisia sovelluskohteita ja sovellustapoja, kuinka käsitellä erilaisia suureita ja niihin liittyviä todennäköisyysjakaumia. Nämä voivat mennä melko nopeasti aika monimutkaisiksikin, mutta edellä kuvatun kaltaiset yksinkertaiset laskelmat ovat vielä tehtävissä pohjimmiltaan kynällä ja paperilla.

Jatkopohdintaa sovelluskohteista#

Ehdollinen todennäköisyys on sangen mielenkiintoinen aihe, koska sen avulla saadaan yhdistettyä uusi ja yksityiskohtaisempi tieto jo olemassa olevaan yleisempään tietoon. Ehdollinen todennäköisyys auttaa myös muodostamaan loogisen viitekehyksen sille ajatukselle, että lähes kaikki vastaantulevat asiat riippuvat jostain taustalla vaikuttavista ilmiöistä ja ovat näin ollen ehdollisia niille.

Esimerkiksi, kuntotutkija saattaa tietää, että jonkin tietyn vauriotyypin esiintyvyys koko populaatiossa on aika korkea. Jos paikan päällä tehdyt selvitykset kuitenkin vaikuttavat juuri kyseisen tilanteen olevan yleistä tilannetta parempi tai huonompi, niin miten nämä kaksi eri asiaa saadaan silloin yhdistettyä toisiinsa? Matemaattisesti tämä on mahdollista tehdä Bayesin lauseen avulla, mutta kuntotutkimusten ja rakennusfysiikan kannalta eri menetelmien luokittelukyvyn tarkkuudesta kertovat lukuarvot pääosin puuttuvat.

Sanotaan, että jokin rakenneratkaisu ei täytä vaatimuksia käytännön kohteessa \(P(A)\) = 20 % todennäköisyydellä. Meillä on käytössämme kuitenkin vain kolikon heittoon vertautuvia tutkimusmenetelmä, joiden kyky tunnistaa puutteellinen puutteelliseksi on \(P(B | A)\) = 0,5 ja hyväksyttävä hyväksyttäväksi myös \(P(\bar{B} | \bar{A})\) = 0,5. Tällöin, jos tutkimusmenetelmä nimittää rakenneratkaisun puutteelliseksi, on päivitetty todennäköisyys rakenteen puutteellisuudelle:

\[\begin{split} \begin{align} P(A | B) &= \frac{0,5 \cdot 0,2}{0,5 \cdot 0,2 + (1-0,5) \cdot (1 - 0,2)} \\ &= \frac{0,1}{0,1 + 0,4} \\ &= 0,2 \end{align} \end{split}\]

Todennäköisyys rakenteen puutteellisuudelle ei muuttunut prioritodennäköisyydestä mihinkään! Ymmärryksen määrä ei siis muuttunut tutkimalla rakennetta kolikonheiton tasoisella menetelmällä. Myöskään useamman menetelmän käyttämisestä ei ole hyötyä, ellei kukin menetelmä itsessään pysty tarjoamaan lisätietoa tutkittavasta kohteesta.

Sanotaan, että käyttämämme menetelmä onkin kolikonheittoa parempi ja sen kyky tunnistaa puutteelliset puutteellisiksi on \(P(B|A)\) = 0,6 ja hyväksyttävät hyväksytyiksi on \(P(\bar{B} | \bar{A})\) = 0,7. Tällöin positiivisen testituloksen saatuamme todennäköisyys rakenteen puutteellisuudelle on:

\[\begin{split} \begin{align} P(A | B) &= \frac{0,6 \cdot 0,2}{0,6 \cdot 0,2 + (1 - 0,7) \cdot (1 - 0,2)} \\ &= \frac{0,12}{0,12 + 0,24} \\ &= 0,33 \end{align} \end{split}\]

Positiivisen testituloksen seurauksena todennäköisyys kasvoi hieman (20 % \(\rightarrow\) 33 %). Jos nyt tekisimme vielä toisen vastaavantasoisen ja ensimmäisestä täysin riippumattoman testin, saisimme:

\[\begin{split} \begin{align} P(A | B) &= \frac{0,6 \cdot 0,33}{0,6 \cdot 0,33 + (1 - 0,7) \cdot (1 - 0,33)} \\ &= \frac{0,20}{0,20 + 0,20} \\ &= 0,50 \end{align} \end{split}\]

Kahdella tämän tasoisella toisistaan riippumattomalla testillä päästiin 0,2 todennäköisyydestä 0,5 todennäköisyyteen, kun molempien testien tulokset olivat positiivisia. Kolmas riippumattoman testin positiivinen tulos nostaisi todennäköisyyden arvoon 0,67 ja neljäs arvoon 0,80. Erottelukyvyltään vaatimattomia testejä tarvitaan vahvoihin johtopäätöksiin useita, mikä on mahdollisesta työläydestään huolimatta kuitenkin toteutettavissa oleva strategia.

Loppusanat#

Tässä kirjoituksessa käytiin läpi todennäköisyyden klassinen, frekventistinen ja bayesiläinen tulkinta ja pohdittiin samalla otoskoa ja tulosten hajontaa yksinkertaisessa nopanheittoesimerkissä.

Esitettyjä tilastomatematiikan perusesimerkkejä voidaan kuitenkin soveltaa myös rakennusfysiikan puolelle periaate-esimerkkien luomiseksi siitä, että miten erilaisia data-aineistoja ja testien tuloksia voi arvioida todennäköisyyksien näkökulmasta.

Juuri mistään rakennusfysiikan ja kuntotutkimusten menetelmästä ei kuitenkaan ole yleisesti käytössä bayesiläisen todennäköisyysarvioinnin edellyttämiä tietoja, joista pystyisi laskemaan todennäköisyyksiä yksittäisen rakenneratkaisun puutteellisuudelle. Isossa kuvassa tällaiset arvot olisivat sangen hyödyllisiä ja rakennusalan kannattaisi sellaisia määrittää.